BloomFilter簡單介紹

BloomFilter我們可能經(jīng)常聽到也在使用, 它的特點是如果判斷結(jié)果為"不存在", 則一定不存在; 如果判斷為存在, 則可能存在. 如下圖示例說明當(dāng)我們判斷z元素存在時, 其實是不存在的, 即存在有概率性.

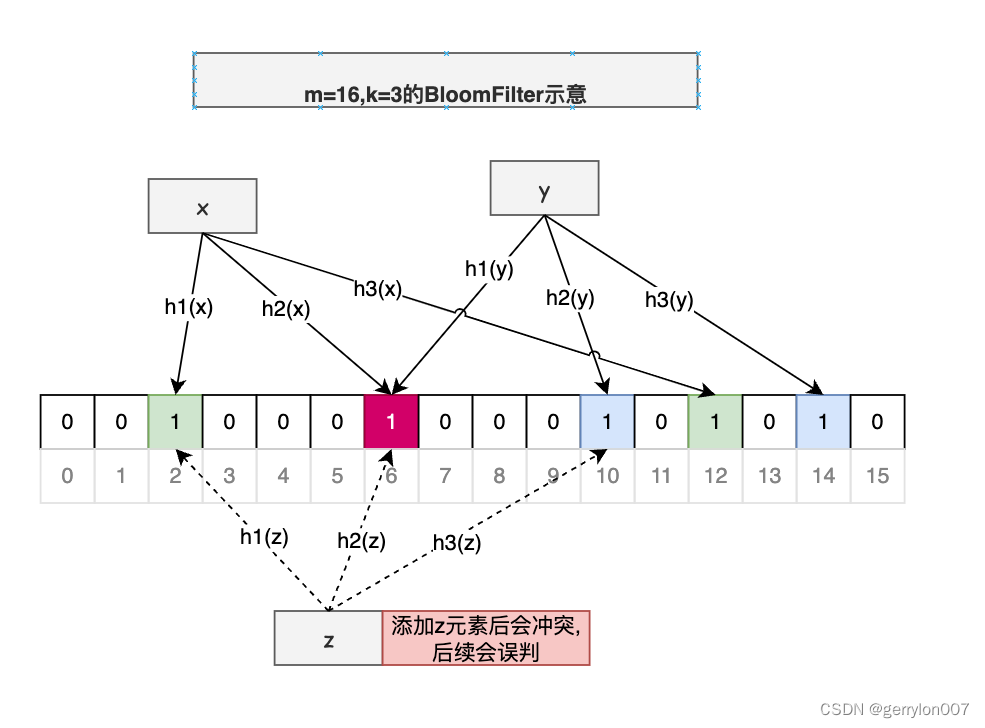
如上圖, 長為m=16的二進制向量, 初始全為0; k=3(即添加一個元素需要將3個bit設(shè)置為1), 對n=3個元素進行添加操作.

BloomFilter幾個關(guān)鍵量定義:
m: 二進制向量大小(多少個二進制位)
n: 要存放的元素個數(shù)
k: 哈希函數(shù)的個數(shù), 或者說每添加一個元素都要進行k次計算
fpp或者簡寫為p: 誤判率(false positive rate), 即 使用bloomfilter判斷為存在時, 但實際不存在的概率

BloomFilter中的數(shù)學(xué)知識

fpp(誤判率/假陽性)的計算

BloomFilter主要的數(shù)學(xué)原理是: 在某一范圍內(nèi)($1<=x<=m)$(x為整數(shù), m通常是很大的, 如$10^6級別$), 任意選取兩個整數(shù)$i,j,i和j可重復(fù)選取$, 則其相等的概率是非常小的: $\frac{m}{m^2}=\frac{1}{m}$

我們假定hash計算是均勻的, 即每次hash會隨機地將m位中的一位設(shè)置為1. 那么:

• 一次hash計算(如$h1(x)$)后, 任一位被 置為1 的概率為: $\frac{1}{m}$
• 一次hash計算(如$h1(x)$)后, 任一位 還是0(即未被置為1) 的概率為: $1?\frac{1}{m}$
• 添加一個元素(如bloomFilter.Add(x), 即執(zhí)行k次hash)后, 任一位還是0的概率為: $(1?\frac{1}{m}{)}^k$
• 添加n個元素后(如上圖中的n=3個元素:x,y,z), 任一位還是0的概率為: $(1?\frac{1}{m}{)}^{kn}$ , 任一位為1的概率為 $1?(1?\frac{1}{m}{)}^{kn}$
• 如果將1個新的元素，添加到已存在n個元素的BloomFilter中，則任一位已經(jīng)為1的概率與上面相同，為：$1?(1?\frac{1}{m}{)}^{kn}$ .
  那么添加這個新元素時, k個比特都為1(相當(dāng)于新元素和已有元素已經(jīng)分不清了)的概率(此即為新插入元素的誤識別率)為：
  $$p=[1?(1?\frac{1}{m}{)}^{kn}{]}^k$$

通常來說, m是一個非常大的數(shù)(1MiB內(nèi)存就有$2^{20}\times 8\approx 800萬$個bit), 并且我們有: $\underset{x\to \infty }{\lim }(1+x{)}^{\frac{1}{x}}=e$
那么在工程實踐中, 可以認為p的近似值為:
$$\begin{array}{rl}p& =[1?(1?\frac{1}{m}{)}^{kn}{]}^k\\ & =[1?(1?\frac{1}{m}{)}^{?m\times \frac{?kn}{m}}{]}^k\\ & \approx (1?e^{?\frac{kn}{m}}{)}^k(當(dāng)m很大時,將?\frac{1}{m}看作x)\end{array}$$

k的最小值

計算過程參考: https://cs.stackexchange.com/questions/132088/how-is-the-optimal-number-of-hashes-is-derived-in-bloom-filter

已經(jīng)遺忘的知識:

1. 求導(dǎo)公式: $(\ln x{)}^{{}^{\prime }}=\frac{1}{x}$
2. 求導(dǎo)公式: $({\mathbf{e}}^{nx}{)}^{{}^{\prime }}=n{\mathbf{e}}^{nx}$

在某些情況下, 我們對n, m, 的值可以給一個估算值, 以此來獲得最小的p(即盡可能準確判斷), 那么k就是一個變量了, 問題就變?yōu)榍?$(1?e^{?\frac{kn}{m}}{)}^k$的最小值.
令$f(k)=(1?e^{?\frac{kn}{m}}{)}^k$, 那么
$$\begin{array}{rl}& 兩邊取對數(shù)有:\\ & \ln f(k)=\ln (1?e^{?\frac{kn}{m}}{)}^k=k\ln (1?e^{?\frac{kn}{m}})\\ & 設(shè)g(k)=k\ln (1?e^{?\frac{kn}{m}}),那么:\\ & g{}^{\prime }(k)=\ln (1?e^{?\frac{kn}{m}})+k\frac{\frac{n}{m}{e}^{?\frac{kn}{m}}}{1?e^{?\frac{kn}{m}}}\\ & 令x=e^{?\frac{kn}{m}},x\in (0,1),那么有\\ & h(x)=\ln (1?x)?\frac{x}{1?x}\ln x(注意k用?\frac{m}{n}lnx替換)\\ & =\frac{(1?x)\ln (1?x)?x\ln x}{1?x}(x\in 0,1)\end{array}$$

對 $h(x)=\frac{(1?x)\ln (1?x)?x\ln x}{1?x}(x\in 0,1)$, 不難看出:

1. 當(dāng)$x=\frac{1}{2}時,h(x)=0$
2. 當(dāng)$x>\frac{1}{2}時,h(x)<0$
3. 當(dāng)$x<\frac{1}{2}時,h(x)>0$

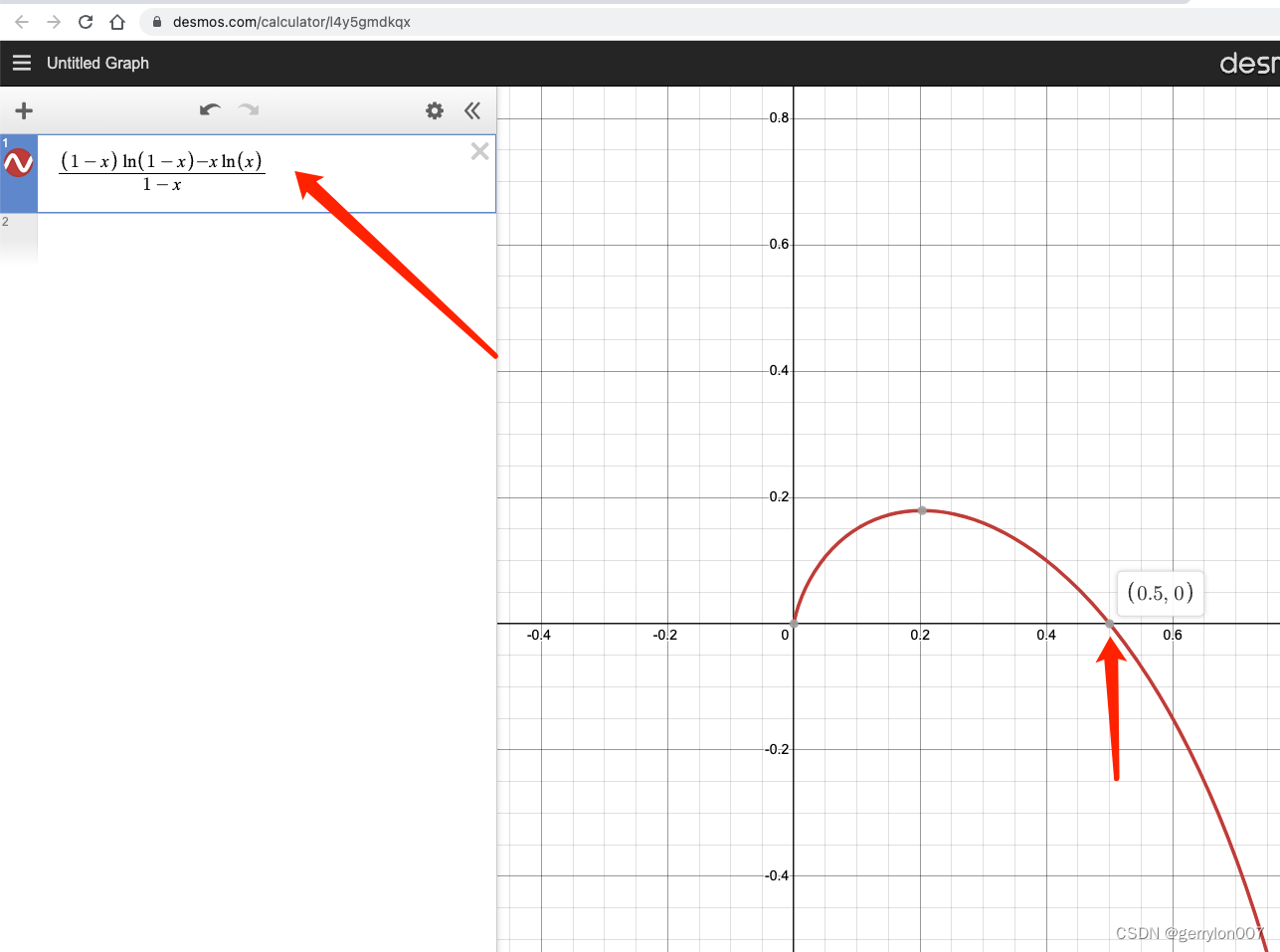
站在巨人的肩膀上, 我們可以直接在這里看:
顯然在$x\in (0,1)范圍內(nèi),當(dāng)x=0.5時,h(x)最小$, 此時$k=\frac{m}{n}ln2$

也就是說:
當(dāng)$k<\frac{m}{n}ln2$時(想象k非常接近0), $x=e^{?\frac{kn}{m}}$會非常接近1, 此時$x>\frac{1}{2}$,
$h(x)<0$ ? f(k)在變小;
當(dāng)$k>\frac{m}{n}ln2$時(想象k非常接近0), $x=e^{?\frac{kn}{m}}$會非常接近0, 此時$x<\frac{1}{2}$,
$h(x)>0$ ? f(k)在變大;
所以$k=\frac{m}{n}ln2$時會使得$f(k)$最小, 即此時p最小.

公式總結(jié)

1. 誤判率公式: $p=[1?(1?\frac{1}{m}{)}^{kn}{]}^k$
2. 誤判率近似公式(當(dāng)m很大時): $p\approx (1?e^{?\frac{kn}{m}}{)}^k$
3. 已知m, n, k的最小值(近似)為: $k=\frac{m}{n}\ln 2\approx 0.7\frac{m}{n}$
4. 已知n, p, 且k取最小時, $m=?\frac{n\ln p}{(ln2{)}^2}$

編程語言實現(xiàn)

golang的實現(xiàn)

https://github.com/bits-and-blooms/bloom

已知n, p求m和k

func EstimateParameters(n uint, p float64) (m uint, k uint) {m = uint(math.Ceil(-1 * float64(n) * math.Log(p) / math.Pow(math.Log(2), 2)))k = uint(math.Ceil(math.Log(2) * float64(m) / float64(n)))return
}

參考

1. https://en.wikipedia.org/wiki/Bloom_filter
2. https://cs.stackexchange.com/questions/132088/how-is-the-optimal-number-of-hashes-is-derived-in-bloom-filter

(完)